Foreword

Nowadays, there is a cool concept out there in the Functional Programming world which is called FRP. It stands for Functional Reactive Programming and is a pretty decent way to make event-driven programs.

The problem with FRP is that, beside Wikipedia, Haskell.org and a few other resources, like Conal Elliott’s papers, we lack learning materials. Getting into FRP is really not trivial and because of the lack of help, you’ll need to be brave to get your feet wet.

Because I found it hard learning it from scratch and because I think it’s a good thing to pass knowledge by, I decided to write a few about it so that people can learn via an easier path.

I’ll be talking about netwire, which is not the de-facto library to use in Haskell, because, eh… we don’t have any. However, netwire exposes a lot of very interesting concepts and helped me to understand more general abstractions. I hope it’ll help you as well. :)

The FRP Thing

Event-driven programming context

In traditional event-driven programming codebase, you’d find constructions such as events polling (when you explicitely retrieve last occurring events), callbacks and event handlers. GLFW is a very famous example of callback uses for event-driven programming. Such functions as glfwSetWindowCloseCallback require you to pass a callback that will be called when the event occurs. While that way to go seems nice, it’s actually error-prone and ill-formed design:

However, it’s not black or white. Callbacks are mandatory. They’re useful, and we’ll see that later on.

What FRP truely is?

FRP is a new way to look at event-driven programming. Instead of representing reaction through callbacks, we consume events over time. Instead of building a callback that will be passed as reaction to the setPushButtonCallback function, we consume and transform events over time. The main idea of FRP could be summed up with the following concepts:

Behaviors

According to Wikipedia, a behavior is the range of actions and mannerisms made by individuals, organisms, systems, or artificial entities in conjunction with themselves or their environment, which includes the other systems or organisms around as well as the (inanimate) physical environment. If we try to apply that to a simple version of FRP that only takes into account the time as external stimulus, a behavior isany kind of value that consumes time. What’s that? Well…

newtype Behavior a = Behavior { stepBehavior :: Double -> a }

A behavior is a simple function from time (Double) to a given value. Let’s take an example. Imagine you want to represent a cube rotating around the X axis. You can represent the actual rotation with a Behavior Rotation, because the angle of rotation is linked to the time:

rotationAngle :: Behavior Rotation
rotationAngle = Behavior $ \t -> rotate xAxis t

Pretty simple, see?! However, it’d would more convenient if we could chose the type of time. We don’t really know what the time will be in the final application. It could be the current UTC time, it could be an integral time (think of a stepped discrete simulation), it could be the monotonic time, the system time, something that we don’t even know. So let’s make our Behavior type more robust:

newtype Behavior t a = Behavior { stepBehavior :: t -> a }

Simple change, but nice improvement.

That is the typical way to picture a behavior. However, we’ll see later that the implementation is way different that such a naive one. Keep on reading.

Events

An event is something happening at some time. Applied to FRP, an event is a pair of time – giving the time of occurrence – and a carried value:

newtype Event t a = Event { getEvent :: (t,a) }

For instance, we could create an event that yields a rotation of 90° around X at 35 seconds:

rotate90XAt35s :: Event Float Rotation
rotate90XAt35s = Event (35,rotate xAxis $ 90 * pi / 180)

Once again, that’s the naive way to look at events. Keep in mind that events have time occurrences and carry values.

Behavior switch

You switch your behavior every time. Currently, you’re reading this paper, but you may go grab some food, go to bed, go to school or whatever you like afterwards. You’re already used to behavior switching because that’s what we do every day in a lifetime.

However, applying that to FRP is another thing. The idea is to express this:

“Given a first behavior, I’ll switch to another behavior when a given event occurs.”

This is how we express that in FRP:

switch :: Behavior t a -> Event t (Behavior t a) -> Behavior t a

Let me decrypt switch for you.

The first parameter, a Behavior t a, is the initial behavior. For instance, currently, you’re reading. That could be the first behavior you’d pass to switch.

The second parameter, an Event t (Behavior t a), is an event that yields a new Behavior t a. Do you start to get it? No? Well then:

switch reading finished

reading is the initial behavior, and finished is an event that occurs when you’re done reading. switch reading finished is then a behavior that equals to reading until finished happens. When it does, switch reading finished extracts the behavior from the event, and uses it instead.

I tend to think switch is a bad name, and I like naming it until:

reading `until` finished

Nicer isn’t it?! :)

Stepping

Stepping is the act of passing the input – i.e. the time t in our case – down to the Behavior t a and extract the resulting a value. Behaviors are commonly connected to each other and form a reactive network.

That operation is also often refered to as reactimation in certain implementations, but is more complex than just stepping the world. You don’t have to focus on that yet, just keep in mind the reactimate function. You might come across it at some time.

Before going on…

Everything you read in that paper until now was just pop-science so that you understand the main idea of what FRP is. The next part will cover a more decent and real-world implementation and use of FRP, especially efficient implementations.

Let’s build a FRP library!

The first common error a lot of programmers make is trying to write algorithms or libraries to solve a problem they don’t even know. Let’s then start with an example so that we can figure out the problem.

Initial program

Setting up

Let’s say we want to be able to control a camera with a keyboard:

Let’s write the Input type:

data Input
  = W
  | S
  | A
  | D
  | R
  | F
  | Quit
    deriving (Eq,Read,Show)

Straight-forward. We also have a function that polls events from IO:

pollEvents :: IO [Input]
pollEvents = fmap treatLine getLine
  where
    treatLine = concatMap (map fst . reads) . words

We use [Input] because we could have several events at the same time (imagine two pressed keys). The function is using dumb implementation in order to abstract over event polling. In your program, you won’t use getLine but a function from SDL or similar.

And the camera:

newtype Camera = Camera { _cameraPosition :: V3 Float } deriving (Eq,Read,Show)

makeLenses ''Camera

V3 is a type from linear. You’ll need that lib then, and import Linear.V3 to make the Camera compile. You’ll also need lens and the GHC TemplateHaskell extension enabled as well as import Control.Lens.

Ok, let’s react to events!

First attempt: the regular and naive one

The idea is to use some kind of state we’ll change on an event. In our case the state is pretty simple:

data AppSt = AppSt {
    _appCamera :: Camera
  } deriving (Eq,Read,Show)
  
makeLenses ''AppSt

updateAppSt :: AppSt -> Input -> Maybe AppSt
updateAppSt appst input = case input of
  W -> Just $ appst & appCamera . cameraPosition . _z -~ 0.1
  S -> Just $ appst & appCamera . cameraPosition . _z +~ 0.1
  A -> Just $ appst & appCamera . cameraPosition . _x -~ 0.1
  D -> Just $ appst & appCamera . cameraPosition . _x +~ 0.1
  F -> Just $ appst & appCamera . cameraPosition . _y -~ 0.1
  R -> Just $ appst & appCamera . cameraPosition . _y +~ 0.1
  Quit -> Nothing

A lot of boilerplate on updateAppSt, but that doesn’t matter that much. The idea is to modify the application state and just return it for all inputs but Quit, in which case we return Nothing to express the wish to quit the application.

I’ve been using that idea for a while. It’s simple, nice and neat, because we don’t spread IO actions in our program logic, which remains then pure. That’s a very good way of doing it, and in most cases, it’ll even be sufficient. However, that idea suffers from a serious issue: it doesn’t scale.

Who has only one camera? No one. You have a camera – maybe more than just one, lights, objects, terrains, AI, sounds, assets, maps and so on and so forth. Our little AppSt type would explode as we add objects. That doesn’t scale at all. You could, though, go on and add all your objects in your AppSt – I did that once, it was a pretty harsh experience.

Furthermore, imagine you want to add a new behavior to the camera, like being able to handle the mouse cursor move – Input being augmented, of course. You’d need to change / add lines in our updateAppSt function. Imagine how messy updateAppSt would be… That would, basically, gather all reactions into a single function. Not neat.

Adding FRP

FRP enables us to use our reactive values as if they are regular values. You can add reactive values, you can substract them, combine them in any way you want. The semantics of your values should be true for the reactive values.

Typically, with FRP, you don’t have event handlers anymore. The codebase can then grow sanely without having to accumulate big states every now and then. FRP applications scale and compose pretty well.

Let’s start with a simple FRP implementation for our example.

Naive FRP implementation

Let’s start with the behavior:

newtype Behavior t a = Behavior { stepBehavior :: t -> a }

How could we implement our camera’s behavior with that? We actually can’t since we don’t have any ways to pass events.

“I guess we could build a Behavior t Camera by passing our Input to the initial function?”

Something like this?

camera inputs = Behavior $ \_ -> -- implement the behavior with inputs

That could be a way to go, yeah. However, how would you implement switching with that? Remember the type of until:

until :: Behavior t a -> Event (Behavior t a) -> Behavior t a

camera is not a behavior, it’s a function from events to a behavior. You have to apply the events on camera in order to get its behavior. Once you’ve done that, you cannot pass events to the next behavior. What a pity. That is more a configured behavior than a behavior consuming inputs / events.

With the current Behavior t a implementation, a behavior network is reduced to a function t -> a, basically. Then, the only stimulus you got from outside is… time. We lack something.

Arrowized behaviors

“A way to forward events?”

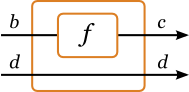
Yes! But more mainly, a way to extend our Behavior t a with inputs! Don’t get me wrong, we are not talking about a reactive value here. We are talking about a reactive relationship:

newtype Behavior t a b = Behavior { stepBehavior :: t -> a -> b }

That’s way better! Our new behavior represents a relationship between two reactive objects. The b is our old a, and the new a is the input! Let’s see what we can do with that.

camera :: Behavior t [Input] Camera
camera = Behavior (const treatEvents)
  where
    treatEvents events
      | W `elem` events = Camera $ V3 0 0 (-0.1)
      | S `elem` events = Camera $ V3 0 0 0.1
      | otherwise = Camera $ V3 0 0 0

That is not exactly what we intented to express. Here, if we push the W button, we just put the camera in V3 0 0 (-0.1), while we’d like to move it forward. That is due to the fact we need switching.

The idea is the following: the initial behavior is idleing. We just don’t do anything. Then, we switch to a given behavior when a given event occurs. We’ll need recursion so that we can ping-pong between behaviors. Let’s write the idleing behavior:

idleing :: Behavior t ([Input],Camera) Camera
idleing = Behavior (const snd)

That behavior requires as input our Input events list and a Camera and simply returns the Camera. Pretty nice.

How do we switch then? We need Event. Consider this:

newtype Event t a = Event { getEvent :: (t,a) }

In order to switch, we need a to be a behavior. In the first place, we’ll create several Event t [Input] and pass them as input to the behavior network. How could we change the [Input] to something more interesting? Simple: Functor!

instance Functor (Event t) where
  fmap f (Event e) = Event (fmap f e)

Note: because of Event t a being a newtype, you should rather use the GHC GeneralizedNewtypeDeriving extension to automatically let GHC infer the instance for you.

newtype Event t a = Event { getEvent :: (t,a) } deriving (Functor)

Then, we can use the Functor instance to change the type of the carried value of the event. That’s great because we don’t change the occurrence time, only the carried value. Transforming events is really important in FRP. We can then transform the [Input] into a single behavior:

inputToBehavior i = case i of
  W -> Behavior $ \_ (_,cam) -> cam & cameraPosition . _z -~ 0.1
  S -> Behavior $ \_ (_,cam) -> cam & cameraPosition . _z +~ 0.1
  A -> -- and so on
  D -> -- and so forth
  F -> -- ;)
  R -> -- ...
  _ -> Behavior $ \_ (_,cam) -> cam

Pretty simple, see? When we push W, we go forward forever. We could have implemented the function above with another until call in order to go back to idleing, making some kind of behavior loop.

However, switching is fairly poorly implemented here. It’s not very efficient, and requires a ton of boilerplate.

Auto

There is a very cool type out there called Auto, used to implement automatons.

newtype Auto a b = Auto { runAuto :: a -> (b,Auto a b) }

An Auto a b is a function-like structure. It has an input and an output. The difference with a regular function is the fact it also has a secondary output, which is another Auto a b. That is, it’s the next automaton to be used.

Auto a b wraps pretty cool concepts, such as locally defined states. It’s also a great ally when implementing switching in a FRP system, because we can easily state that Behavior ≃ Auto. A Behavior is a function from the environment state to the next reactive value, and has also another output representing what to do “next”.

Let’s then change our Behavior type to make it look like a bit more like Auto:

newtype Behavior t a b = Behavior { stepBehavior :: t -> a -> (b,Behavior t a b) }

Yeah, that’s it! That’s a pretty good start!

Useful abstractions

Before going on, I’d like to introduce those scary abstractions you are afraid of. Because they’re actually not. They’re all simple. At least for Haskell purposes.

Note: I do know we could simply use the GeneralizedNewtypeDeriving` extension but I want to detail all the implementation, so we’ll see how to implement all the nice abstractions.

Arrow

Arrows are a generalization of functions along the axis of computation. A computation has inputs and outputs. So does a behavior.

Although arrows are not really used in Haskell, they’re ultra simple (themselves and the common combinators built over the abstraction) and useful in some cases.

In order to implement arrows, we need to provide code for both the arr function, which type is arr :: (Arrow a) => (b -> c) -> a b c and first, which type is first :: (Arrow a) => a b c -> a (b,d) (c,d). arr is used to lift a common function into the arrowized version, and first takes an arrow which takes a value as input and exposes an arrow that takes a pair as input, applying the given function on the first value of the pair. Let’s implement that:

instance Arrow (Behavior t) where
  arr f = fix $ \r -> Behavior $ \t a -> (f a,r)
  first f = Behavior $ \t (b,d) ->
    let (c,fn) = stepBehavior f t b
    in ((c,d),first fn)

Category

A category basically exposes two concepts: composition and identity. In our case, the identity represents a constant behavior in time and the composition composes two behaviors in time. Let’s implement Category by providing implementation for both id and (.):

instance Category (Behavior t) where
  id = arr id
  x . y = Behavior $ \t a ->
    let (yr,yn) = stepBehavior y t a
        (xr,xn) = stepBehavior x t yr
    in (xr,xn . yn)

Note: because of Prelude exporting specialized implementation of id and (.) – the function ones – you should hide them in order to implement Category:

import Prelude hiding ( (.), id )

Semigroup

A semigroup is a pretty cool algebraic structure used in Haskell to represent “anything that associates”. It exposes an associative binary function over a set. In the case of behaviors, if two behaviors output semigroup values, we can associates the behaviors to build a single one.

A Semigroup is implemented via a single typeclass method, (<>). Let’s do that for behaviors:

instance (Semigroup b) => Semigroup (Behavior t a b) where
  x <> y = Behavior $ \t a ->
    let (xr,xn) = stepBehavior x t a
        (yr,yn) = stepBehavior y t a
    in (xr <> yr,xn <> yn)

Simple and neat.

Functor

You might already know that one since I talked about it a few lines ago, but let’s write the instance for our Behavior:

instance Functor (Behavior t a) where
  fmap f b = Behavior $ \t a ->
    let (br,bn) = stepBehavior b t a
    in (f br,fmap f bn)

Pretty cool eh?

Applicative

A very known one too. Let’s see how we could implement Applicative:

instance Applicative (Behavior t a) where
  pure = arr . const
  f <*> x = Behavior $ \t a ->
    let (fr,fn) = stepBehavior f t a
        (xr,xn) = stepBehavior x t a
    in (fr xr,fn <*> xn)

Profunctor

This one is special. You don’t have to know what a profunctor is, but eh, you should, because profunctors are pretty simple to use in Haskell, and are very useful. I won’t explain what they are – you should have a look at this article for further details.

If you do know them, here’s the implementation for dimap:

instance Profunctor (Behavior t) where
  dimap l r x = Behavior $ \t a ->
    let (xr,xn) = stepBehavior x t (l a)
    in (r xr,dimap l r xn)

Inhibition

Bare concept

Behaviors consume environment state and have outputs. However, they sometimes just don’t. They don’t output anything. That could be the case for a behavior that only emits during a certain period of time. It could also be the case for a signal function that’s defined on a given interval: what should we output for values that lie outside?

Such a scenario is called inhibition. There’re several solutions to implement inhibition. The simplest and most famous one is by using Maybe as a wrapper over the output. Like the following:

Behavior t a (Maybe b)

If (Maybe b) is Nothing, the output is undefined, then the behavior inhibits.

However, using a bare Maybe exposes the user directly to inhibition. There’s another way to do that:

newtype Behavior t a b = Behavior { stepBehavior :: t -> a -> Maybe (b,Behavior t a b) }

Here we are. We have behaviors that can inhibit. If a behavior doesn’t inhibit, it returns Just (output,nextBehavior), otherwise it outputs Nothing and inhibits forever.

Exercise: try to reimplement all the above abstractions with the new type of Behavior.

We can add a bunch of other interesting functions:

Inhibition-related combinators

dead :: Behavior t a b
dead = Behavior $ \_ _ -> Nothing

one :: b -> Behavior t a b
one x = Behavior $ \_ _ -> Just (x,dead)

dead is a behavior that inhibits forever. That is, it doesn’t produce any value at any time.

one x produces x once, and then inhibits forever. That’s a nice combinator to use when you want to pulse values in time. We’ll see later that it’s very useful to represent discrete events, like key presses or mouse motion.

However, inhibiting can be useful. For instance, we can implement a new kind of behavior switching using inhibition. Let’s try to implement a function that takes two behaviors and switches to the latter when the former starts inhibiting:

revive :: Behavior t a b -> Behavior t a b -> Behavior t a b
revive x y = Behavior $ \t a -> case stepBehavior x t a of
  Just (xr,xn) -> return (xr,revive xn y)
  Nothing -> stepBehavior y t a

(~>) :: Behavior t a b -> Behavior t a b -> Behavior t a b
(~>) = revive

(~>) is a handy alias to revive. Then, a ~> b is a behavior that is a until it inhibits, afterwhile it’s b. Simple, and useful.

In netwire, revive – or (~>) – is (-->). There’s also an operator that does the opposite thing: (>--). a >-- b is a until b starts producing – i.e. until b doesn’t inhibit anymore.

Exercise: write the implementatof of (>~), our version for netwire’s (>--).

Behaviors revisited

Now you have a better idea of how you could implement a behavior, let’s talk about netwire’s one.

netwire’s behavior type is called Wire. It’s actually:

Wire s e m a b

s is the session time – it’s basically a type that’s used to extract time. e is the inhibition value. m is a inner monad – yes, you can use monadic code within netwire, which is not really useful actually, except for Reader, I guess. And a and b are respectively inputs and outputs.

“What is that inhibition type?”

Yeah, netwire doesn’t use Maybe for inhibition. Picture Wire as:

newtype Wire s e m a b = Wire { stepWire :: s -> a -> m (Either e (b,Wire s e m a b)) }

Instead of using Maybe (b,Wire s e m a b), it uses Either. Some functions require e to be a Monoid. I guess netwire uses that to accumulate during inhibition. I don’t see decent use cases of such a feature, but it’s there. I tend to use this kind of wire in all my uses of netwire:

Wire s () Identity a b -- I think this is the most common type of wire

Keep in mind that although you can set m to IO, it’s not what netwire – and FRP – was designed for.

Events

What about events? Well, netwire exposes events as a home-made Maybe:

data Event a
  = Event a
  | NoEvent
    deriving (Eq,Show)

instance Functor Event where
  fmap f e = case e of
    Event a -> Event (f a)
    NoEvent -> NoEvent

That’s actually enough, because we can attach Event a to time occurences with Behavior t b a. You’ll find every now and then functions using Wire s e m (Event a) b, for instance. You should get used to that as you write toy examples, and real-world ones, of course.

In the end

What a trek… As you can see, we were able to approach netwire’s implementation understanding pretty closely. There are a few concepts I haven’t covered – like intrinsic switches, continuable switches, deferred switches… – but I don’t pretend having a comprehensive FRP article. You’ll have to dig in a bit more ;)

I’ll write another article about FRP and netwire to implement the camera example with netwire so that you can have a concrete example.

↑ Getting into netwire
Sun Mar 15 00:00:00 2015 UTC